三角函数: 正弦 , 余弦 , 正切 , 正割(连线) , 余割(连线) , 余切(连线) 三角函数 是数学 里向顶顶常见个一类关于角度 的函数 。三角函数奈直角三角形 个内角同道伊个两边个比值 相关联起来的,阿可以等价个用啦哈单位圆 有关个各种线段个长度来落定义。常见三角函数包括正弦函数 (
sin
{\displaystyle \sin }
余弦函数 (
cos
{\displaystyle \cos }
正切函数 (
tan
{\displaystyle \tan }
tg
{\displaystyle \operatorname {tg} }
航海学 、测绘学 、工程学等其他学科中,还会用到如余切函数 、正割函数 、余割函数 另外个三角函数 。不一色一样个三角函数之间个关系可以通过几何直观或者计算得出,叫做三角恒等式 。
18世纪开始,随着解析几何等分析学工具个引进,数学家们开始对三角函数进行分析学上的研究。牛顿来伊个1669年个《分析学》一书中畀出了正弦搭余弦函数个无穷级数 表示。卡琳拿牛顿 做出来个结果讲畀詹姆斯·格列高里听,伊进一步证明出来个正切等三角函数个无穷级数。莱布尼兹 拉1673年左右也独立得到了迭一结果[1] :162-163 。欧拉 个《无穷小量分析引论 》(Introductio in Analysin Infinitorum ,1748年)对建立三角函数个分析处理做了最主要个贡献,伊定义三角函数为无穷级数,写出个欧拉公式 ,还有使用接近现代个英文 字母sin. 、cos. 、tan. 、cot. 、sec. 和cosec. 。
a, b, h为角A个对边、邻边搭斜边 在直角三角形 中仅有锐角 (大小在0到90度之间的角)三角函数个定义。给定一个锐角
θ
{\displaystyle \theta }
θ
{\displaystyle \theta }
θ
{\displaystyle \theta }
a
{\displaystyle a}
b
{\displaystyle b}
h
{\displaystyle h}
θ
{\displaystyle \theta }
正弦 是对边与斜边个比值:
sin
θ
=
a
h
{\displaystyle \sin {\theta }={\frac {a}{h}}}
θ
{\displaystyle \theta }
余弦 是邻边与斜边个比值:
cos
θ
=
b
h
{\displaystyle \cos {\theta }={\frac {b}{h}}}
θ
{\displaystyle \theta }
正切 是对边与邻边个比值:
tan
θ
=
a
b
{\displaystyle \tan {\theta }={\frac {a}{b}}}
θ
{\displaystyle \theta }
余切 是邻边与对边个比值:
cot
θ
=
b
a
{\displaystyle \cot {\theta }={\frac {b}{a}}}
θ
{\displaystyle \theta }
正割 是斜边与邻边个比值:
sec
θ
=
h
b
{\displaystyle \sec {\theta }={\frac {h}{b}}}
θ
{\displaystyle \theta }
余割 是斜边与对边个比值:
csc
θ
=
h
a
{\displaystyle \csc {\theta }={\frac {h}{a}}}
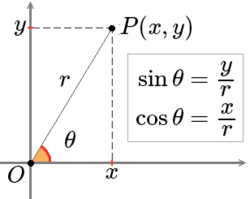
设
p
{\displaystyle p}
x
{\displaystyle x}
y
{\displaystyle y}
Template:Math 中个一个点,
θ
{\displaystyle \theta }
O
x
→
{\displaystyle {\vec {Ox}}}
O
P
→
{\displaystyle {\vec {OP}}}
r
=
x
2
+
y
2
>
0
{\displaystyle r={\sqrt {x^{2}+y^{2}}}>0}
P
{\displaystyle P}
O
{\displaystyle O}
θ
{\displaystyle \theta }
正弦:
sin
θ
=
y
r
,
{\displaystyle \sin \theta ={\frac {y}{r}},}
正切:
tan
θ
=
y
x
,
{\displaystyle \tan \theta ={\frac {y}{x}},}
正割:
sec
θ
=
r
x
,
{\displaystyle \sec \theta ={\frac {r}{x}},}
余弦:
cos
θ
=
x
r
,
{\displaystyle \cos \theta ={\frac {x}{r}},}
余切:
cot
θ
=
x
y
,
{\displaystyle \cot \theta ={\frac {x}{y}},}
余割:
csc
θ
=
r
y
.
{\displaystyle \csc \theta ={\frac {r}{y}}.}
箇浪可以对0到360度个角度定义三角函数。要注意个是以上个定义侪只拉定义式有意义个辰光成立。比方讲当
x
=
0
{\displaystyle x=0}
y
x
{\displaystyle {\frac {y}{x}}}
r
x
{\displaystyle {\frac {r}{x}}}
啦哈直角坐标系平面高头画f (x ) = sin(x )和f (x ) = cos(x )函数个图。 从几何定义中可以推导出咾多三角函数个性质。比方讲,正弦函数、正切函数、余切函数搭余割函数是奇函数,余弦函数搭正割函数是偶函数。正弦搭余弦函数个图像形状一样(看正手边个图),可以看作是沿坐标横轴平移得到个两个函数。正弦搭余弦函数关于
x
=
π
4
{\displaystyle x={\frac {\pi }{4}}}
弗同个三角函数之间存在咾多对任意个角度取值侪成立个等式,被称为三角恒等式。其中最著名个是毕达哥拉斯恒等式 ,伊说明对于任何角,正弦个平方加上余弦个平方总是1。箇好从斜边为1个直角三角形用勾股定理 得出哉。用符号表示出来个言语,毕达哥拉斯恒等式 为:
sin
2
x
+
cos
2
x
=
1.
{\displaystyle \sin ^{2}\!x+\cos ^{2}\!x=1.}
↑ 莫里斯·克莱因 著,朱学贤,申又枨,叶其孝 译(2002).《古今数学思想》第二册.上海科学技术出版社.ISBN 9787532361731 .