三体问题
外观
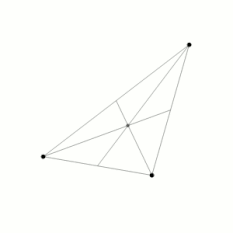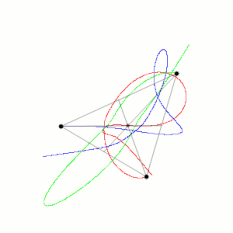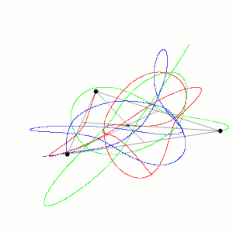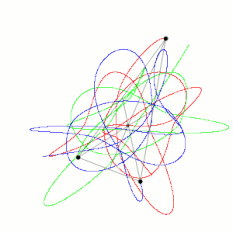
三体问题(英语:Three-body problem)是天体力学当中个基本力学模型。
内容
[编辑]伊指个是三个质量、初始位置搭初始速度侪是任意个好看成是质点个天体,勒拉三個物事当中个万有引力个作用下头个运动规律问题。
现在已经晓得,三体问题呒没精确个解,也就是呒没办法预测所有三体问题个数学情景,只有当中某几种特殊情况好研究。
比方讲勒拉太阳系当中,考虑太阳、地球搭月球个运动,伊拉当中通过万有引力相吸引。假使讲箇三颗星球侪看成质点,而且忽略脱其他星球个引力,箇末太阳、地球搭月球个运动也就可以畀看成是三体问题。
历史
[编辑]1887年,为仔庆祝自家个60岁生日,瑞典国王奥斯卡二世花钞票赞助仔一项竞赛,求个是太阳系个稳定性问题个解答,箇是三体问题个一個变种。
法国数学家庞加莱简化仔箇只问题,提出限制性三体问题:也就是加上仔当中两個球体个质量邪氣大,让第三個球体个质量完全弗会得对伊产生啥扰动箇个条件。面对箇只问题,庞加莱用仔伊自家发明个相态图理论,阿末发现仔混沌理论。虽然箇个方法根本呒没畀出一個完整个答案,伊个研究让人有蛮深个印象,让伊勒拉1888年捞着奖金。
庞加莱发现箇只系统个演变经常是混沌个,也就是讲如果初始状态浪有一個小个扰动,比方讲一个物事个初始位置有些小个变化,箇末后些来个状态可能会得有邪氣大个弗同。假使讲箇个小个变化测弗出,箇末我伲就呒没办法估出伊阿末个状态。
当中个一位裁判,数学家卡尔·魏尔施特拉斯表扬伊:“箇个研究弗好真正看作是对箇个要求个问题个完善解答,但是伊个重要性标志天体力学个一个新时代个诞生。”
